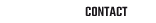PDF version of the IGS2016 summerschool program:
- IGS2016 Summer School Flyer: IGS2016_summerschool.pdf
| Saturday, June 18 | |
| 08:30-09:00 | IGS Summer School Registration |
| 09:00-10:30 | Course 1: Computational Aspects of Mappings by Noam Aigerman and Shahar Kovalsky (Weizmann Institute) |
| 10:30-11:00 | Coffee Break |
| 11:00-12:00 | Course 2: Inverse Problems in Computational Design by Bernhard Thomaszewski (Disney Research Zurich) |
| 12:00-13:30 | Lunch |
| 13:30-15:00 | Course 3: Optimization in Geometry Processing by David Bommes (RWTH Aachen) and Justin Solomon (MIT) |
| 15:00-15:30 | Coffee Break |
| 15:30-16:30 | Course 4: Quad Mesh Generation by Marcel Campen (New York University) |
| 16:30-17:30 | Course 5: Skinning: Real-time Shape Deformation by Alec Jacobson (Columbia University) |
| 18:30-21:00 | Social Event at Restaurant "Luise" |
| Sunday, June 19 | |
| 08:45-09:00 | IGS Summer School Registration |
| 09:00-10:30 | Course 6: Laplace-Beltrami: The Swiss Army Knife of Geometry Processing by Etienne Vouga (UT Austin) |
| 10:30-11:00 | Coffee Break |
| 11:00-12:00 | Course 7: Pyramid Algorithms by Ron Goldman (Rice University) |
| 12:00-13:30 | Lunch |
| 13:30-15:00 | Course 8: Simplification and Approximation by Pierre Alliez (INRIA Sophia Antipolis) |
| 15:00-15:30 | Coffee Break |
| 15:30-17:00 | Course 9: Representations and Applications of Tangential Vector Fields by Mirela Ben-Chen and Omri Azencot (Technion) |
| 17:00-18:00 | Course 10: Projective Geometric Algebra: A Swiss Army Knife for Graphics and Games by Charles Gunn (TU Berlin) |
| 18:00 | Closing Session |
Course Details
Course 1 Computational Aspects of Mappings Noam Aigerman and Shahar Kovalsky (Weizmann Institute)
Abstract: Maps are fundamental to Geometry Processing, and play a key role in a wide spectrum of applications, e.g., deformations, parameterizations, shape matching, remeshing, and texturing. In this tutorial we will review both the theory and practice of methods for computing maps that satisfy important properties such as energy-minimization, bounded distortion, and injectivity. We will demonstrate how these concepts take a particularly simple form when applied to piecewise-linear maps, the natural choice for triangular (and tetrahedral) meshes. The tutorial will only assume knowledge of linear algebra, which will be shown to be more than enough to handle discrete analogs of deep geometric concepts such as harmonicity, rigidity and conformality.
Brief Biography: Noam Aigerman is a PhD student in the department of Computer Science and Applied Math at the Weizmann Institute of Science, Israel. His main research interests are Geometry Processing and numerical optimization, focusing primarily on mapping and parameterization algorithms. He holds a B.Sc. and an M.Sc. in Computer Science from the Hebrew University of Jerusalem. Shahar Kovalsky has graduated his PhD studies in the department of Computer Science and Applied Math at the Weizmann Institute of Science, Israel. His main research interests are in numerical optimization, computer graphics and vision, and in particular, applications of convex optimization to geometry processing. Shahar holds a B.Sc. in Mathematics and B.Sc. and M.Sc. in Electrical Engineering from Ben-Gurion University.
Course 2 Inverse Problems in Computational Design Bernhard Thomaszewski (Disney Research Zurich)
Abstract: Physical simulation is the cornerstone of many computational design tools. However, when designing physical artifacts with complex forms and functions, we often need to solve inverse problems, i.e., invert the simulation in order to compute design parameters that lead to the desired system state or behavior. In this short course, I will introduce inverse problems in the context of computational design and discuss how they can be solved using constrained optimization. In order to illustrate these concepts, we will look at design problems involving elastic deformations and mechanical motion.
Brief Biography: Bernhard Thomaszewski is a Research Scientist at Disney Research Zurich, where he leads the group on Computational Design and Digital Fabrication. He obtained his Master’s degree (Diplom) and PhD (Dr. rer. nat.) in Computer Science from the University of Tübingen. Prior to joining Disney Research, he was a postdoctoral researcher at ETH Zürich, where he is an adjunct lecturer today. Bernhard's research interests are in the areas of computational design, digital fabrication, and computer animation. His current focus is on design tools that allow non-expert users to create functional content for digital fabrication devices.
Course 3 Optimization in Geometry Processing David Bommes (RWTH Aachen) and Justin Solomon (MIT)
Abstract: Countless techniques in geometry processing can be described variationally, that is, as the minimization or maximization of an objective function measuring shape properties. Algorithms for parameterization, mapping, quad meshing, alignment, smoothing, and other tasks can be expressed and solved in this powerful language. With this motivation in mind, this tutorial will summarize typical use cases for optimization in geometry processing. In particular, we will show how procedures for generating, editing, and comparing shapes can be expressed variationally and will summarize computational tools for solving the relevant optimization problems in practice. Along the way, we will highlight tools for prototypical problems in this class, including algorithms for unconstrained/constrained/convex optimization, lightweight schemes recently popularized in the machine learning literature, and procedures for relaxing discrete problems. The only background assumed is basic calculus and linear algebra.
Brief Biography: David Bommes is a junior professor in the Aachen Institute for Advanced Study in Computational Engineering Science at RWTH Aachen University, studying mesh generation and optimization. Justin Solomon is an assistant professor of Electrical Engineering and Computer Science at MIT, studying geometric correspondence and related optimization problems.
Course 4 Quad Mesh Generation Marcel Campen (New York University)

Abstract: Triangle meshes are a well-known and quite predominant representation for surfaces and other kinds of geometric data. Their simplicial structure makes handling, processing, and modification relatively easy and convenient. In certain domains though, there is a strong preference for meshes composed of quadrilateral rather than triangular elements. Their specific structure allows for alignment to the directions of principal curvature, stress or strain, the characteristic directions of PDEs on surfaces, etc. These properties provide advantages particularly in areas such as animation and simulation. There is a decades-long history of manual and assisted quad mesh generation; a process that can be highly time consuming and expensive. Recent advances in the field of geometry processing have spawned a variety of powerful and flexible automatic and semi-automatic quad mesh generation techniques that are now starting to improve efficiency in this area. In this tutorial, after a look at the historic development, we discuss in detail the modern techniques that enable the generation of quad meshes with respect to a variety of objectives and quality criteria. These may involve properties such as the size, anisotropy, orientation, and alignment of the individual quad elements, as well as the local and global structure of the quad mesh in terms of connectivity and topology. Despite the remarkable results to date, automatic quad mesh generation remains to be a very active research area. We elaborate on the open problems that are waiting to be addressed, related to reliability, robustness, optimality, and the move towards the incorporation of higher-level aspects. Finally, an outlook on the generalization of the discussed techniques to the next dimension is given, where hexahedral meshes are desired for the discretization of volumes when modeling just the surface is insufficient.
Brief Biography: Marcel Campen is a postdoctoral researcher at New York University (Courant Institute), working with Denis Zorin and Claudio Silva. He received his doctoral degree in 2014 from RWTH Aachen University, where he worked with Leif Kobbelt. He is the author of numerous papers on the topic of quad mesh and quad layout generation and optimization, and is currently working on the challenging open problems in this area.
Course 5 Skinning: Real-time Shape Deformation Alec Jacobson (Columbia University)
Abstract: The intended audience of this course are computer graphics practitioners and researchers, from technical directors to programmers or students. This course serves both as an implementation recipe for state-of-the-art deformation techniques as well as summary of the most recent research and unsolved challenges. Assuming a modest technical background (college-level linear algebra and geometry), we introduce the basics of real-time skinning and then dive into cutting-edge methods found in academic research and used in industry production.
Brief Biography: Alec Jacobson is a post-doctoral researcher at Columbia University working with Prof. Eitan Grinspun. He received a PhD in Computer Science from ETH Zurich, and an MA and BA in Computer Science and Mathematics from the Courant Institute of Mathematical Sciences, New York University. His thesis on real-time deformation techniques for 2D and 3D shapes was awarded the ETH Medal and the Eurographics Best PhD award. Leveraging ideas from differential geometry and finite-element analysis, his work in geometry processing improves exposure of geometric quantities, while his novel user interfaces reduce human effort and increase exploration. He has published several papers in the proceedings of SIGGRAPH. He leads development of the widely used geometry processing library, libigl, winner of the 2015 SGP software award.
Course 6 Laplace-Beltrami: The Swiss Army Knife of Geometry Processing Etienne Vouga (UT Austin)

Abstract: A remarkable variety of basic geometry processing tools can be expressed in terms of the Laplace-Beltrami operator on a surface—understanding these tasks in terms of fundamental PDEs such as heat flow, Poisson equations, and eigenvalue problems leads to an efficient, unified treatment at the computational level. The central goal of this tutorial is to show students 1. how to build the Laplacian on a triangle mesh, and 2. how to use this operator to implement a diverse array of geometry processing tasks. We will also discuss alternative discretizations of the Laplacian (e.g., on point clouds and polygon meshes), recent developments in discretization (e.g., via power diagrams), and important properties of the Laplacian in the smooth setting that become essential in geometry processing (e.g., existence of solutions, boundary conditions, etc.).
Brief Biography:
Etienne Vouga is an assistant professor of computer science at the University of Texas at Austin. He received his PhD from Columbia University in 2013, where he worked with Eitan Grinspun, and worked at Harvard University in 2014 as a postdoc, applying ideas of discrete differential geometry and geometry processing to problems involving crumpling and growth of thin shells. Etienne's research interests are applying geometric principles to physical simulation and inverse designs problems involving surfaces and shells.
Etienne Vouga, Keenan Crane, and Justin Solomon developed the tutorial on the Laplace-Beltrami operator together for the SGP Summer School.
Etienne will be presenting the tutorial in place of Keenan Crane, who for reasons outside his control cannot attend the summer school.
Course 7 Pyramid Algorithms Ron Goldman (Rice University)
Abstract: Pyramid algorithms are dynamic programming procedures for organizing, visualizing, and analyzing recursive algorithms for freeform curves and surfaces. Important examples of pyramid algorithms include:
- Neville’s algorithm for Lagrange interpolation,
- de Casteljau’s evaluation algorithm and subdivision procedures for Bezier approximation,
- de Boor’s evaluation algorithm and knot insertion procedures for B-spline curves and surfaces.
In this lecture we provide an introduction to pyramid algorithms, and we show how to use pyramid algorithms to understand the organization and properties of a variety of fundamental procedures for freeform curves and surfaces.
Brief Biography: Ron Goldman is a Professor of Computer Science at Rice University in Houston, Texas. Professor Goldman received his B.S. in Mathematics from the Massachusetts Institute of Technology in 1968 and his M.A. and Ph.D. in Mathematics from Johns Hopkins University in 1973. Professor Goldman’s current research interests lie in the mathematical representation, manipulation, analysis and reconstruction of shape using computers. His work includes research in computer aided geometric design, solid modeling, computer graphics, subdivision, polynomials and splines. He is particularly interested in algorithms for polynomial and piecewise polynomial curves and surfaces, as well as in applications of algebraic and differential geometry to geometric modeling. He most recent focus is on the uses of quaternions and Clifford algebras in computer graphics. https://www.cs.rice.edu/~rng/
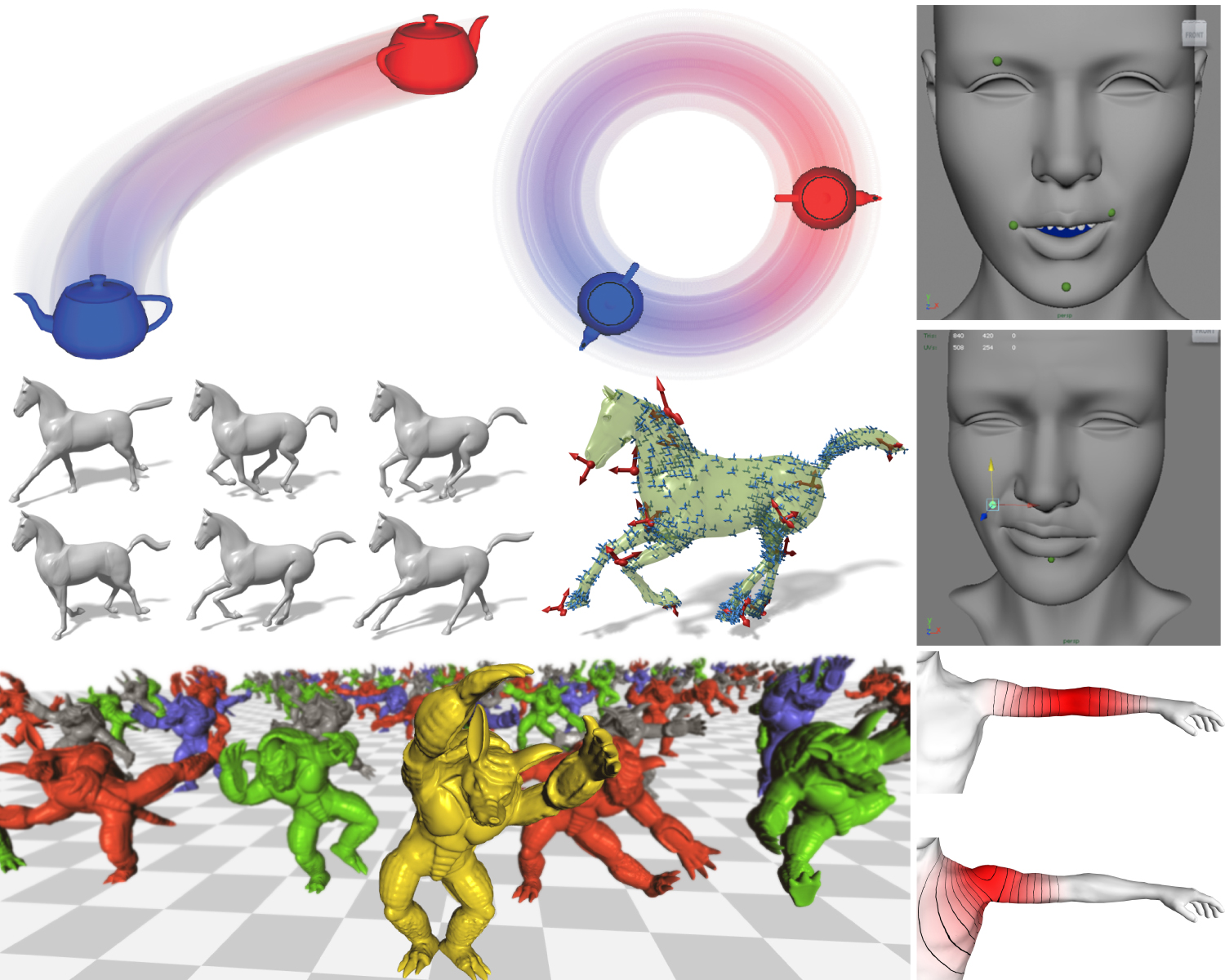
Course 8 Simplification and Approximation Pierre Alliez (INRIA Sophia Antipolis)
Abstract: Mesh simplification and surface approximation are two core topics in geometry processing. In this lecture we will review the main approaches and error metrics used for mesh simplification and approximation of surfaces. We will distinguish between greedy algorithms (coarse-to-fine versus fine-to-coarse) and approaches involving local or global optimization. We will also review the approaches that come with guarantees such as global error bound or topology.
Brief Biography: Pierre Alliez is Senior Researcher and team leader at Inria Sophia-Antipolis - Mediterranee. He has authored many scientific publications and several book chapters on mesh compression, surface reconstruction, mesh generation, surface remeshing and mesh parameterization. He is an associate editor of the Computational Geometry Algorithms Library (http://www.cgal.org) and an associate editor of the ACM Transactions on Graphics. He was awarded in 2005 the EUROGRAPHICS young researcher award for his contributions to computer graphics and geometry processing. He was co-chair of the Symposium on Geometry Processing in 2008, of Pacific Graphics in 2010 and Geometric Modeling and Processing 2014. He was awarded in 2011 a Starting Grant from the European Research Council on Robust Geometry Processing. https://team.inria.fr/titane/pierre-alliez/
Course 9 Representations and Applications of Tangential Vector Fields Mirela Ben-Chen and Omri Azencot (Technion)
Abstract: Tangent vector fields are fundamental to many applications in geometry processing. In this tutorial we discuss various representations of tangent vector fields on triangle meshes (vertex- and face-based, discrete 1-forms and operator representations) and present a sample of applications (vector field driven deformation, vector field design, the advection equation and vector field visualization). The goal of the tutorial is to give the audience a view of the state-of-the-art of the field and, if time permits, also discuss interesting open problems. The only background we will assume is linear algebra and multi-variate calculus.
Brief Biographies: Omri Azencot is a PhD candidate at the Computer Science Department at the Technion, advised by Assistant Professor Mirela Ben-Chen. His research is focused on differential operators and fluid simulation on curved domains. Mirela Ben-Chen is an Assistant Professor at the Computer Science Department at the Technion, Israel. She has received her PhD from the same department, and was a Fulbright Scholar at Stanford. Her main research interest is geometry processing, focusing on shape analysis and discrete differential geometry.
Course 10 Projective Geometric Algebra: A Swiss Army Knife for Graphics and Games Charles Gunn (TU Berlin)
Abstract: A short, informal introduction to a newly-developed toolkit for doing euclidean geometry, based on half-forgotten 19th century discoveries. In three words: quaternions on steroids. Level of difficulty: the treatment will be aimed at entering graduate students who after a day of tutorials might prefer to be relaxing in a beer garden.
Brief Biographies: In three words: projective geometry evangelist. Degrees: M. S. (Math., UNC-CH) and Ph. D. (Math., TU-Berlin). Work history: Pixar, the Geometry Center (U. of MN.), Green Meadow Waldorf School, and TU-Berlin. Wide experience in 3D scene graph development (jReality) driven by interests in interactive visualization and mathematical movie- and 3D print-making. Also active as writer and lecturer to raise awareness of projective geometry as a tool for inner and outer development. URL: page.math.tu-berlin.de/~gunn, email: projgeom (at) gmail.com. Lives near Berlin with wife and daughter.